I numeri della fotografia
Argomenti trattati:
Il diaframma
Il fattore di CROP
Lunghezze focali a confronto
Il rapporto di riproduzione
La diffrazione
Profondità di campo, distanza iperfocale e circolo di confusione
....::::....::::....::::.... ....::::....::::....::::.... ....::::....::::....::::.... ....::::....::::....::::....
Il diaframma
E' quel elemento interno all'obiettivo, che determina con la propria apertura/chiusura, la quantità di luce che raggiunge il sensore (nell'unità di tempo).
Negli Obiettivi, il diaframma può essere regolato su diverse aperture, distribuite regolarmente su una scala di intervalli detti numeri f (f/numero) aperture diframmali o più semplicemente diaframmi; l'intervallo tra i diversi valori del diaframma viene definito 'stop'.
I numeri f sono calcolati e ordinati in modo tale che chiudendo il diaframma di uno 'scatto' , cioè di 1 stop; si dimezza la quantità di luce che colpisce il sensore.
I numeri f esprimono il rapporto tra la lunghezza focale dell'obiettivo e il diametro dell'apertura del diaframma (pertanto a valori più bassi di f corrispondono aperture di diaframma più ampie).
E' facilmente intuibile quindi che la sequenza dei valori di numeri f è una progressione geometrica legata all'area del cerchio di apertura del diaframma (se si dimezza l'area del cerchio, si dimezza la luce a parità di lunghezza focale).
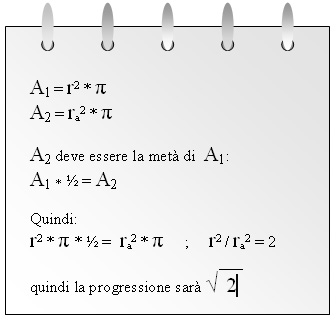
La progressione ha quindi ragione 'radice quadrata di 2' (ossia circa 1,414) e i valori possono essere:
f/1 f/1,4 f/2 f/2,8 f/4 f/5,6 f/8 f/11 f/16 f/22 f/32 f/45 f/64
Quale influenza ha il diaframma nello scatto di una fotografia ?
- Determina i tempi di esposizione:
diaframmi chiusi (quindi valori f/ alti) richiedono tempi di esposizione più lunghi; viceversa diaframmi aperti (bassi valori f/) , permettendo un maggior ingresso di luce, richiedono tempi di esposizione corti.
- determina la profondità di campo:
diaframmi chiusi aumentano la profondità di campo (ossia aumenta la porzione di spazio 'a fuoco' che si estende davanti all'obiettivo); diaframmi aperti isolano maggiormente il soggetto della fotografia mettendo a fuoco una porzione limitata di spazio.
Il fattore di CROP
E' un dato tecnico che caratterizza una macchina fotografica digitale; nello specifico è relativo alla dimensione del sensore in relazione alla dimensione della 'vecchia' pellicola.
I sensori non 'full frame' (APS-C), ossia con dimensioni inferiori alla pellicola 24x36 mm, catturano una porzione minore dell’immagine proiettata dalla lente.


Essendo ogni obiettivo caratterizzato da un propria lunghezza focale, per poter confrontare tra loro gli angoli di campo di obiettivi differenti agganciati a fotocamere differenti; occorre NORMALIZZARE la lunghezza focale moltiplicandola per il fattore di CROP.
Esempio: un obiettivo da 18mm agganciato ad una fotocamera con CROP = 1.6 inquadrerà la stessa porzione di scena ripresa con un obiettivo 28mm agganciato ad una fotocamera full frame con CROP = 1
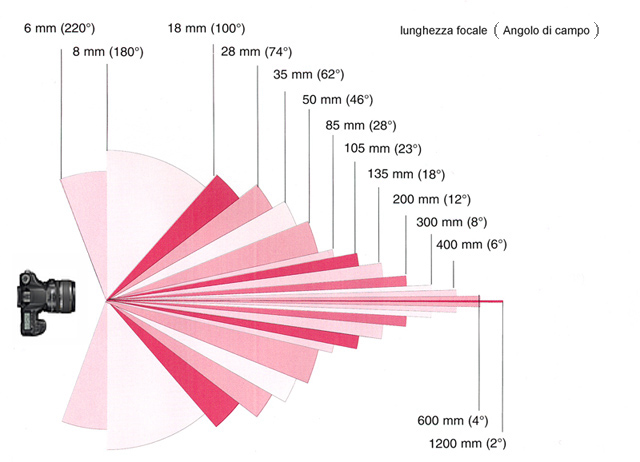
Vediamo ora come si calcola il fattore di CROP:

Per le fotocamere (non full frame) Canon il fattore è 1.6x , nelle reflex Nikon è 1.5x.
Lunghezze focali a confronto
Visto il fattore di CROP, possiamo ora fare un ulterire passo in avanti, confrontando tra loro differenti fotocamere,a parità di ottica utilizzata, per valutare la porzione di scena inquadrata (normalizzata ad una certa risoluzione della foto finale).
Entra in questo caso in gioco la densità dei pixell sul sensore, quindi la dimensione effettiva dei pixell stessi.
In post produzione, definiamo come punto di arrivo una foto da 10MP, cercando di 'zoomare' digitalmente quanto più possibile.
Scattiamo una foto con differenti fotocamere, utilizzando lo stesso obiettivo a focale fissa (Canon EF 400mm).
Tra una fotocamera Full Frame (EOS 5D MarkII) ed una APS-C (EOS 40D) la differenza di campo inquadrato è data unicamente dal fattore di CROP.
Se però prendiamo in considerazione la porzione relativa a soli 10 mega pixell, il fattore di CROP che avremo sulla FF è di soli 1,4.
fattore di crop nettamente superiore lo avremo utilizzando un'immagine (normalizzata a 10MP) scattata con la EOS 7D; vantando quest'ultima una dimensione dei pixell di soli 4 micrometri.
La seguente tabella riassume questi concetti:

Mentre la seguente immagine, ci fa capire quale porzione di spazio saremo in grado di sfruttare ottenendo come risultato della post produzione una immagine a 10MP non interpolati.
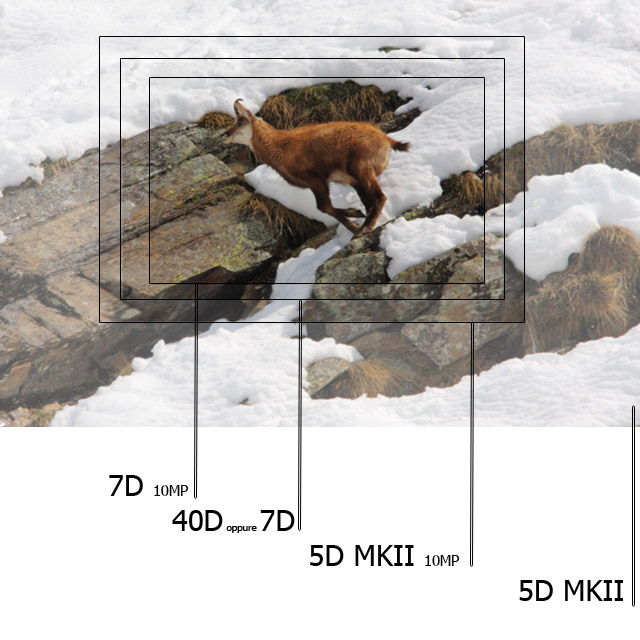
Ben inteso che qui non si sta valutando la qualità della foto finale (rumorosa o meno, con più o meno profondità di campo,ecc...) ma si tratta solo di fare un raffronto sulla base dei pixell di un sensore.
Il rapporto di riproduzione
è la relazione tra le dimensioni fisiche del soggetto fotografato e le dimensioni del sensore.
Anche in questo caso, come per il fattore di Crop visto in precedenza, come termine di paragone si prende il formato della pellicola 35mm, e quindi un rapporto 1:1 equivale a fotografare un oggetto largo 36mm e alto 24mm.
Con un rapporto 2:1 l'immagine catturata sarà 2 volte più grande del reale (sarà quindi inquadrata un'area del soggetto grande la metà 18x12mm) e così via.
Il rapporto 1:1 nelle digitali con sensore APS-C (più piccolo di 24x36) sarà ovviamente proporzionato ale dimensioni del sensore.

Obiettivi con rapporti compresi tra 1:1 e 10:1 (foto fino a 10 volte più grande del reale -solo 1/10 del soggetto è inquadrato-) vengono utilizzati per la macrofografia
Obiettivi con rapporti più grandi ad esempio 1:2 , 1:3 , 1:4 vengono utilizzati per la fotografia ravvicinata e sono considerati 'Close-Up'.
La diffrazione
produce una sorta di effetto stella sui punti luminosi di una scena (ad es sole, lampioni, fari, ...).
La diffrazione è un fenomeno fisico che, causa interferenza costruttiva - distruttiva delle onde elettromagnetiche (anche la luce è un'onda elettromagnetica), genera 'frange' distinte.
Facendo passare un fascio di luce attraverso una fessura, l'immagine che si potrà osservare su di uno schermo posto dierto la fessura sarà composta da una serie di linee.
Per lo stesso principio, se la luce viene fatta passare attraverso una fessura quadrata, si otterrà una sorta di croce sullo schermo.
E' facile intuire quinidi che, aumentando il numero di lati del foro attraverso cui si fa passare la luce, si ottiene una stella formata da tante fasce luminose quanti sono i lati del foro.

Osserviamo questo fenomeno anche in fotografia, essendo l'obiettivo un elemento in cui la luce attraversandolo, si scontra con il diaframma.
Ecco perchè fotografando sorgenti luminose con diaframma molto chiuso, si generano 'stelle' luminose.
Obiettivi con diaframma composto da un numero pari di lamelle, generano stelle con tante fasce quante sono le lamelle.
Gli obiettivi con diaframma composto da un numero dispari di lamelle (ad esempio 7), generano 'stelle' a 14 fasce luminose (in quanto le fasce luminose non si sommano 2 a 2 come in diaframmi pari).
Profondità di campo, distanza iperfocale e circolo di confusione
La profondità di campo è quella porzione di spazio (che si estende davanti all'obiettivo) in cui gli oggetti inquadrati appaiono nitidi (sia in fase di scatto che ovviamente in fase di stampa).
La profondità di campo ha un'importanza fondamentale in fotografia e permette al fotografo di interpretare una scena esaltando alcuni particolari oppure armonizzare i vari soggetti tra loro.
Gli aspetti e le formule matematiche che regolano la profondità di campo sono molte; partiamo dalle seguenti due formule base per calcolare i limiti anteriore e posteriore della PDC:
Limite anteriore -> HxD/(H+D)
Limite posteriore -> HxD/(H-D)
dove H è la distanza iperfocale e D è la distanza di ripresa.
Dobbiamo obbligatoriamente dettagliare cosa si intende per distanza iperfocale.
La distanza iperfocale è la distanza di messa a fuoco che permette di estendere la profondità di campo dalla metà della distanza di ripresa, all'infinito.
Se infatti l'obiettivo viene messo a fuoco alla distanza iperfocale, il limite anteriore e posteriore dello sazio 'a fuoco' diventa:
HxH/(H+H) = H/2
e
HxH/(H-H) = HxH/0 = infinito
Il valore della distanza iperfocale dipende da due fattori : dalla lunghezza focale dell'obiettivo e dall' apertura di diaframma. questi due fattori sono in relazione tra loro secondo la seguente formula.
H = fxf/NxC
dove f è la lunghezza focale dell'obiettivo in mm (ad es 50mm 100mm ...), N l'apertura relativa (f/4 f/16 ...) e C il diametro del cerchio di confusione.
Ecco che dobbaimo ora passare dal concetto di 'cerchio di confusione'.
Con una stampa 20x25 cm, osservata ad una distanza di 25 centimetri, un normale occhio umano distingue 5 linee per millimetro: quindi 0,2 millimetri.
Vaiazioni del punto di fuoco che rimangono all'interno del circolo di confusione, non vengono percepiti dall'occhio umano e quindi l'immagine appare nitida.
Un' immagine catturata da un sensore full frame 24x36 mm che viene stampata in formato 20x25 cm , deve essere ingrandita di 7,56 volte.
Il circolo di confusione che si dovrà avere sul sensore affinchè la fuoco risulti a fuoco, dovrà essere quindi calcolato come 0,2 mm / 7,56 = 0,026 mm.
Nel caso di immagine catturata da sensore APS-C 22.5x15.0 mm, il circolo di confusione dovrà essere di 0.016 mm
Utilizzando le formule di cui sopra, vediamo ora alcuni esempi:
focale 10mm
diaframma f/4 -> distanza iperfocale 1,7 mt
diaframma f/8 -> distanza iperfocale 0,83 mt
diaframma f/16 -> distanza iperfocale 0,42 mt
diaframma f/22 -> distanza iperfocale 0,30 mt
focale 50mm
diaframma f/4 -> distanza iperfocale 41,7 mt
diaframma f/8 -> distanza iperfocale 20,8 mt
diaframma f/16 -> distanza iperfocale 10,4 mt
diaframma f/22 -> distanza iperfocale 7,6 mt
focale 100mm
diaframma f/4 -> distanza iperfocale 167 mt
diaframma f/8 -> distanza iperfocale 83 mt
diaframma f/16 -> distanza iperfocale 42 mt
diaframma f/22 -> distanza iperfocale 30 mt
focale 300mm
diaframma f/4 -> distanza iperfocale 1500 mt
diaframma f/8 -> distanza iperfocale 750 mt
diaframma f/16 -> distanza iperfocale 375 mt
diaframma f/22 -> distanza iperfocale 273 mt
Conclusioni...
- I grandangolari hanno una profondità di campo molto estesa.
Fotografia eseguita con una macchina APS-C; obiettivo 10mm; f/4; soggetto a 5mt = avremo una scena a fuoco da 1mt circa all'infinito
In queste condizioni, tutti gli elementi della scena saranno tra loro armonizzati.

- I teleobiettivi hanno una profondità di campo assolutamente selettiva.
Fotografia eseguita con una macchina APS-C; obiettivo 100mm; f/4; soggetto a 5mt = avremo una scena a fuoco da 4.8 mt a 5.1 mt (ossia solo per una trentina di centimetri).
In queste condizioni, sarà dato risalto al solo elemento inquadrato.

Il diaframma
Il fattore di CROP
Lunghezze focali a confronto
Il rapporto di riproduzione
La diffrazione
Profondità di campo, distanza iperfocale e circolo di confusione
....::::....::::....::::.... ....::::....::::....::::.... ....::::....::::....::::.... ....::::....::::....::::....
Il diaframma
E' quel elemento interno all'obiettivo, che determina con la propria apertura/chiusura, la quantità di luce che raggiunge il sensore (nell'unità di tempo).
Negli Obiettivi, il diaframma può essere regolato su diverse aperture, distribuite regolarmente su una scala di intervalli detti numeri f (f/numero) aperture diframmali o più semplicemente diaframmi; l'intervallo tra i diversi valori del diaframma viene definito 'stop'.
I numeri f sono calcolati e ordinati in modo tale che chiudendo il diaframma di uno 'scatto' , cioè di 1 stop; si dimezza la quantità di luce che colpisce il sensore.
I numeri f esprimono il rapporto tra la lunghezza focale dell'obiettivo e il diametro dell'apertura del diaframma (pertanto a valori più bassi di f corrispondono aperture di diaframma più ampie).
E' facilmente intuibile quindi che la sequenza dei valori di numeri f è una progressione geometrica legata all'area del cerchio di apertura del diaframma (se si dimezza l'area del cerchio, si dimezza la luce a parità di lunghezza focale).

La progressione ha quindi ragione 'radice quadrata di 2' (ossia circa 1,414) e i valori possono essere:
f/1 f/1,4 f/2 f/2,8 f/4 f/5,6 f/8 f/11 f/16 f/22 f/32 f/45 f/64
Quale influenza ha il diaframma nello scatto di una fotografia ?
- Determina i tempi di esposizione:
diaframmi chiusi (quindi valori f/ alti) richiedono tempi di esposizione più lunghi; viceversa diaframmi aperti (bassi valori f/) , permettendo un maggior ingresso di luce, richiedono tempi di esposizione corti.
- determina la profondità di campo:
diaframmi chiusi aumentano la profondità di campo (ossia aumenta la porzione di spazio 'a fuoco' che si estende davanti all'obiettivo); diaframmi aperti isolano maggiormente il soggetto della fotografia mettendo a fuoco una porzione limitata di spazio.
Il fattore di CROP
E' un dato tecnico che caratterizza una macchina fotografica digitale; nello specifico è relativo alla dimensione del sensore in relazione alla dimensione della 'vecchia' pellicola.
I sensori non 'full frame' (APS-C), ossia con dimensioni inferiori alla pellicola 24x36 mm, catturano una porzione minore dell’immagine proiettata dalla lente.


Essendo ogni obiettivo caratterizzato da un propria lunghezza focale, per poter confrontare tra loro gli angoli di campo di obiettivi differenti agganciati a fotocamere differenti; occorre NORMALIZZARE la lunghezza focale moltiplicandola per il fattore di CROP.
Esempio: un obiettivo da 18mm agganciato ad una fotocamera con CROP = 1.6 inquadrerà la stessa porzione di scena ripresa con un obiettivo 28mm agganciato ad una fotocamera full frame con CROP = 1

Vediamo ora come si calcola il fattore di CROP:

Per le fotocamere (non full frame) Canon il fattore è 1.6x , nelle reflex Nikon è 1.5x.
Lunghezze focali a confronto
Visto il fattore di CROP, possiamo ora fare un ulterire passo in avanti, confrontando tra loro differenti fotocamere,a parità di ottica utilizzata, per valutare la porzione di scena inquadrata (normalizzata ad una certa risoluzione della foto finale).
Entra in questo caso in gioco la densità dei pixell sul sensore, quindi la dimensione effettiva dei pixell stessi.
In post produzione, definiamo come punto di arrivo una foto da 10MP, cercando di 'zoomare' digitalmente quanto più possibile.
Scattiamo una foto con differenti fotocamere, utilizzando lo stesso obiettivo a focale fissa (Canon EF 400mm).
Tra una fotocamera Full Frame (EOS 5D MarkII) ed una APS-C (EOS 40D) la differenza di campo inquadrato è data unicamente dal fattore di CROP.
Se però prendiamo in considerazione la porzione relativa a soli 10 mega pixell, il fattore di CROP che avremo sulla FF è di soli 1,4.
fattore di crop nettamente superiore lo avremo utilizzando un'immagine (normalizzata a 10MP) scattata con la EOS 7D; vantando quest'ultima una dimensione dei pixell di soli 4 micrometri.
La seguente tabella riassume questi concetti:

Mentre la seguente immagine, ci fa capire quale porzione di spazio saremo in grado di sfruttare ottenendo come risultato della post produzione una immagine a 10MP non interpolati.

Ben inteso che qui non si sta valutando la qualità della foto finale (rumorosa o meno, con più o meno profondità di campo,ecc...) ma si tratta solo di fare un raffronto sulla base dei pixell di un sensore.
Il rapporto di riproduzione
è la relazione tra le dimensioni fisiche del soggetto fotografato e le dimensioni del sensore.
Anche in questo caso, come per il fattore di Crop visto in precedenza, come termine di paragone si prende il formato della pellicola 35mm, e quindi un rapporto 1:1 equivale a fotografare un oggetto largo 36mm e alto 24mm.
Con un rapporto 2:1 l'immagine catturata sarà 2 volte più grande del reale (sarà quindi inquadrata un'area del soggetto grande la metà 18x12mm) e così via.
Il rapporto 1:1 nelle digitali con sensore APS-C (più piccolo di 24x36) sarà ovviamente proporzionato ale dimensioni del sensore.

Obiettivi con rapporti compresi tra 1:1 e 10:1 (foto fino a 10 volte più grande del reale -solo 1/10 del soggetto è inquadrato-) vengono utilizzati per la macrofografia
Obiettivi con rapporti più grandi ad esempio 1:2 , 1:3 , 1:4 vengono utilizzati per la fotografia ravvicinata e sono considerati 'Close-Up'.
La diffrazione
produce una sorta di effetto stella sui punti luminosi di una scena (ad es sole, lampioni, fari, ...).
La diffrazione è un fenomeno fisico che, causa interferenza costruttiva - distruttiva delle onde elettromagnetiche (anche la luce è un'onda elettromagnetica), genera 'frange' distinte.
Facendo passare un fascio di luce attraverso una fessura, l'immagine che si potrà osservare su di uno schermo posto dierto la fessura sarà composta da una serie di linee.
Per lo stesso principio, se la luce viene fatta passare attraverso una fessura quadrata, si otterrà una sorta di croce sullo schermo.
E' facile intuire quinidi che, aumentando il numero di lati del foro attraverso cui si fa passare la luce, si ottiene una stella formata da tante fasce luminose quanti sono i lati del foro.

Osserviamo questo fenomeno anche in fotografia, essendo l'obiettivo un elemento in cui la luce attraversandolo, si scontra con il diaframma.
Ecco perchè fotografando sorgenti luminose con diaframma molto chiuso, si generano 'stelle' luminose.
Obiettivi con diaframma composto da un numero pari di lamelle, generano stelle con tante fasce quante sono le lamelle.
Gli obiettivi con diaframma composto da un numero dispari di lamelle (ad esempio 7), generano 'stelle' a 14 fasce luminose (in quanto le fasce luminose non si sommano 2 a 2 come in diaframmi pari).
Profondità di campo, distanza iperfocale e circolo di confusione
La profondità di campo è quella porzione di spazio (che si estende davanti all'obiettivo) in cui gli oggetti inquadrati appaiono nitidi (sia in fase di scatto che ovviamente in fase di stampa).
La profondità di campo ha un'importanza fondamentale in fotografia e permette al fotografo di interpretare una scena esaltando alcuni particolari oppure armonizzare i vari soggetti tra loro.
Gli aspetti e le formule matematiche che regolano la profondità di campo sono molte; partiamo dalle seguenti due formule base per calcolare i limiti anteriore e posteriore della PDC:
Limite anteriore -> HxD/(H+D)
Limite posteriore -> HxD/(H-D)
dove H è la distanza iperfocale e D è la distanza di ripresa.
Dobbiamo obbligatoriamente dettagliare cosa si intende per distanza iperfocale.
La distanza iperfocale è la distanza di messa a fuoco che permette di estendere la profondità di campo dalla metà della distanza di ripresa, all'infinito.
Se infatti l'obiettivo viene messo a fuoco alla distanza iperfocale, il limite anteriore e posteriore dello sazio 'a fuoco' diventa:
HxH/(H+H) = H/2
e
HxH/(H-H) = HxH/0 = infinito
Il valore della distanza iperfocale dipende da due fattori : dalla lunghezza focale dell'obiettivo e dall' apertura di diaframma. questi due fattori sono in relazione tra loro secondo la seguente formula.
H = fxf/NxC
dove f è la lunghezza focale dell'obiettivo in mm (ad es 50mm 100mm ...), N l'apertura relativa (f/4 f/16 ...) e C il diametro del cerchio di confusione.
Ecco che dobbaimo ora passare dal concetto di 'cerchio di confusione'.
Con una stampa 20x25 cm, osservata ad una distanza di 25 centimetri, un normale occhio umano distingue 5 linee per millimetro: quindi 0,2 millimetri.
Vaiazioni del punto di fuoco che rimangono all'interno del circolo di confusione, non vengono percepiti dall'occhio umano e quindi l'immagine appare nitida.
Un' immagine catturata da un sensore full frame 24x36 mm che viene stampata in formato 20x25 cm , deve essere ingrandita di 7,56 volte.
Il circolo di confusione che si dovrà avere sul sensore affinchè la fuoco risulti a fuoco, dovrà essere quindi calcolato come 0,2 mm / 7,56 = 0,026 mm.
Nel caso di immagine catturata da sensore APS-C 22.5x15.0 mm, il circolo di confusione dovrà essere di 0.016 mm
Utilizzando le formule di cui sopra, vediamo ora alcuni esempi:
focale 10mm
diaframma f/4 -> distanza iperfocale 1,7 mt
diaframma f/8 -> distanza iperfocale 0,83 mt
diaframma f/16 -> distanza iperfocale 0,42 mt
diaframma f/22 -> distanza iperfocale 0,30 mt
focale 50mm
diaframma f/4 -> distanza iperfocale 41,7 mt
diaframma f/8 -> distanza iperfocale 20,8 mt
diaframma f/16 -> distanza iperfocale 10,4 mt
diaframma f/22 -> distanza iperfocale 7,6 mt
focale 100mm
diaframma f/4 -> distanza iperfocale 167 mt
diaframma f/8 -> distanza iperfocale 83 mt
diaframma f/16 -> distanza iperfocale 42 mt
diaframma f/22 -> distanza iperfocale 30 mt
focale 300mm
diaframma f/4 -> distanza iperfocale 1500 mt
diaframma f/8 -> distanza iperfocale 750 mt
diaframma f/16 -> distanza iperfocale 375 mt
diaframma f/22 -> distanza iperfocale 273 mt
Conclusioni...
- I grandangolari hanno una profondità di campo molto estesa.
Fotografia eseguita con una macchina APS-C; obiettivo 10mm; f/4; soggetto a 5mt = avremo una scena a fuoco da 1mt circa all'infinito
In queste condizioni, tutti gli elementi della scena saranno tra loro armonizzati.

- I teleobiettivi hanno una profondità di campo assolutamente selettiva.
Fotografia eseguita con una macchina APS-C; obiettivo 100mm; f/4; soggetto a 5mt = avremo una scena a fuoco da 4.8 mt a 5.1 mt (ossia solo per una trentina di centimetri).
In queste condizioni, sarà dato risalto al solo elemento inquadrato.

Voti
L'assegnazione di un voto è possibile solo se si è utenti registrati.
Per favore loggati o registrati.
Per favore loggati o registrati.
Nessun voto pervenuto

